A common method of reducing the complexity of n-gram modeling is using the Markov Property. The Markov Property states that the probability of future states depends only on the present state, not on the sequence of events that preceded it. This concept can be elegantly implemented using a Markov Chain storing the probabilities of transitioning to a next state.
Let’s look at a simple example of a Markov Chain that models text using bigrams. The following code creates a list of bigrams from a piece of text.
>>> s = "I am Sam. Sam I am. I do not like green eggs and ham."
>>> tokens = s.split(" ")
>>> bigrams = [(tokens[i],tokens[i+1]) for i in range(0,len(tokens)-1)]
>>> bigrams
[('I', 'am'), ('am', 'Sam.'), ('Sam.', 'Sam'), ('Sam', 'I'), ('I', 'am.'), ('am.', 'I'), ('I', 'do'), ('do', 'not'), ('not', 'like'), ('like', 'green'), ('green', 'eggs'), ('eggs', 'and'), ('and', 'ham.')]
Listing the bigrams starting with the word I results in:
I am, I am., and I do. If we were to use this data to predict a word that
follows the word I we have three choices and each of them has the same
probability (1/3) of being a valid choice. Modeling this using a Markov Chain
results in a state machine with an approximately 0.33 chance of transitioning to
any one of the next states.

We can add additional transitions to our Chain by considering additional bigrams
starting with am, am., and do. In each case, there is only one possible
choice for the next state in our Markov Chain given the bigrams we know from our
input text. Each transition from one of these states therefore has a 1.0
probability.
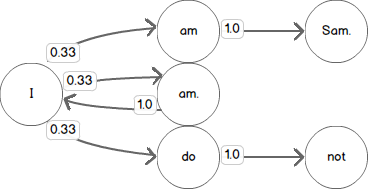
Now, given a starting point in our chain, say I, we can follow the transitions
to predict a sequence of words. This sequence follows the probability
distribution of the bigrams we have learned. For example, we can randomly sample
from the possible transitions from I to arrive at the next possible state in
the machine.
>>> import random
>>> random.sample(['am', 'am.', 'do'], 1)
['am.']
>>> random.sample(['am', 'am.', 'do'], 1)
['do']
Making the first transition, to do, we can sample from the possible states
following do.
>>> random.sample(['am', 'am.', 'do'], 1)
['do']
Writing a Markov Chain
We have all the building blocks we need to write a complete Markov Chain
implementation. The implementation is a simple dictionary with each key being
the current state and the value being the list of possible next states. For
example, after learning the text I am Sam. our dictionary would look like
this.
{
'I': ['am'],
'am': ['Sam.'],
}
And after adding the text Sam I am. our dictionary would look like this.
{
'I': ['am', 'am.'],
'am': ['Sam.'],
'Sam': ['I'],
}
We can implement a basic Markov Chain that creates a bigram dictionary using the following code.
class MarkovChain:
def __init__(self):
self.memory = {}
def _learn_key(self, key, value):
if key not in self.memory:
self.memory[key] = []
self.memory[key].append(value)
def learn(self, text):
tokens = text.split(" ")
bigrams = [(tokens[i], tokens[i + 1]) for i in range(0, len(tokens) - 1)]
for bigram in bigrams:
self._learn_key(bigram[0], bigram[1])
if __name__ == '__main__':
m = MarkovChain()
m.learn('I am Sam. Sam I am. I do not like green eggs and ham.')
print(m.memory)
>>> python markov_chain.py
{'I': ['am', 'am.', 'do'],
'Sam': ['I'],
'Sam.': ['Sam'],
'am': ['Sam.'],
'am.': ['I'],
'and': ['ham.'],
'do': ['not'],
'eggs': ['and'],
'green': ['eggs'],
'like': ['green'],
'not': ['like']}
We can then transition to a new state in our Markov Chain by randomly choosing a next state given the current state. If we do not have any information on the current state we can randomly pick a state to start in.
def _next(self, current_state):
next_possible = self.memory.get(current_state)
if not next_possible:
next_possible = self.memory.keys()
return random.sample(next_possible, 1)
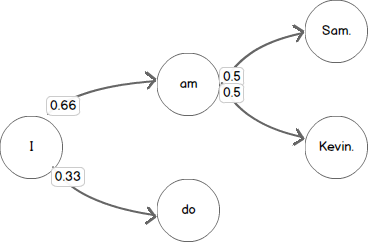
The transition probabilities between states naturally become weighted as we
learn more text. For example, in the following sequence we learn a few
sentences with the same bigrams and in the final state we are twice as likely to
choose am as the next word following I by randomly sampling from the next
possible states.
>>> from markov_chain import MarkovChain
>>> m = MarkovChain()
>>> m.learn('I am Sam.')
>>> m.memory
{'I': ['am'], 'am': ['Sam.']}
>>> m.learn('I am Kevin.')
>>> m.memory
{'I': ['am', 'am'], 'am': ['Sam.', 'Kevin.']}
>>> m.learn('I do.')
>>> m.memory # Twice as likely to follow 'I' with 'am' than 'do'.
{'I': ['am', 'am', 'do'], 'am': ['Sam.', 'Kevin.']}
The state machine produced by our code would have the probabilities in the following figure.
Finally, we can ask our chain to print out some text of an arbitrary length by following the transitions between the text we have learned.
def babble(self, amount, state=''):
if not amount:
return state
next_word = self._next(state)
if not next_word:
return state
return state + ' ' + self.babble(amount - 1, next_word)
Putting it all together we have a simple Markov Chain that can learn bigrams and babble text given the probability of bigrams that it has learned. Markov Chain’s are a simple way to store and query n-gram probabilities. Full source code for this example follows.
The Implementation
import random
class MarkovChain:
def __init__(self):
self.memory = {}
def _learn_key(self, key, value):
if key not in self.memory:
self.memory[key] = []
self.memory[key].append(value)
def learn(self, text):
tokens = text.split(" ")
bigrams = [(tokens[i], tokens[i + 1]) for i in range(0, len(tokens) - 1)]
for bigram in bigrams:
self._learn_key(bigram[0], bigram[1])
def _next(self, current_state):
next_possible = self.memory.get(current_state)
if not next_possible:
next_possible = self.memory.keys()
return random.sample(next_possible, 1)[0]
def babble(self, amount, state=''):
if not amount:
return state
next_word = self._next(state)
return state + ' ' + self.babble(amount - 1, next_word)